Tutorial – Sequential Code on your FPGA

Using Process (in VHDL) or Always Block (in Verilog) with Clocks

If you are unfamiliar with the basics of a Process or Always Block, go back and read this page about how to use a Process/Always Block to write Combinational Code. Writing sequential code is different. For sequential logic, a Process/Always Block can have at most two signals in its sensitivity list. If the Process/Always Blocks uses an asynchronous reset, it will have two signals in the sensitivity list. If the FPGA designer uses a synchronous reset or no reset at all, it will only have one signal in the sensitivity list. For now we will look at the example that uses no reset at all:

-- VHDL Example of Sequential Logic:
process (i_clock)
begin
  if rising_edge(i_clock) then
    and_gate <= input_1 and input_2;
  end if;
end process;

// Verilog Example of Sequential Logic:
always @ (posedge i_clock)
  begin
    and_gate <= input_1 & input_2;
  end

At first glance, this code would appear to do the exact same thing as the combinational example that we saw previously. That’s mostly true, except for the fact that we have instantiated sequential logic here, rather than just combinational logic. By using the: if rising_edge(i_clock) statement (in VHDL) or @ (posedge i_clock), we are telling to tools to create a register (Flip-Flop). This will in fact behave slightly differently than the combinational example; the value of and_gate will only be updated on the clock edges! In this case we used the keyword rising_edge for the VHDL example or the equivalent posedge for the Verilog Example which means when the clock goes from a 0 to a 1. This is almost always the edge that you will be using to trigger your flip-flop logic.

Sequential logic is what the majority of your FPGA design will be constructed with. Registers are the work-horses of FPGAs and ASICs, as they are able to retain a signal’s value for a clock cycle. Sequential logic is necessary to create state-machine logic, memory interfaces, bus controllers, and just about every piece of your design will have at least some sequential logic. And all of that sequential logic lives in Processes or Always Blocks.

Let’s look at another example. How many clock cycles will it take for the value 1 to propagate (pass) from the signal test1 to the signal test4?

-- VHDL Example:
signal test1 : std_logic := '1';
signal test2 : std_logic := '0';
signal test3 : std_logic := '0';
signal test4 : std_logic := '0';

process (i_clock)
begin
  if rising_edge(i_clock) then
    test2 <= test1;
    test3 <= test2;
    test4 <= test3;
  end if;
end process;

// Verilog Example: 
reg test1 = 1'b1;
reg test2 = 1'b0;
reg test3 = 1'b0;
reg test4 = 1'b0;

always @ (posedge i_clock)
  begin
    test2 <= test1;
    test3 <= test2;
    test4 <= test3;
  end

Essentially we are trying to design a flip-flop chain. Such a chain would be drawn out like this:

On the first clock cycle, ALL of the lines get executed at the same time. So you need to fill in the value of test1, test2, and test3 at the beginning of the clock cycle, in order to find out what they will look like for the next clock cycle. The first clock cycle looks like this:

  test2 <= '1'; -- test1
  test3 <= '0'; -- test2
  test4 <= '0'; -- test3

So after the first clock cycle, test2 = 1, test3 = 0, test4 = 0. Let’s look at the next clock cycle:

  test2 <= '1'; -- test1
  test3 <= '1'; -- test2
  test4 <= '0'; -- test3

At the beginning of this clock cycle, test2 was equal to ‘1’, and by the end of the clock cycle this value has propagated to test3. So after the second clock cycle, test2 = 1, test3 = 1, test4 = 0. Let’s look at one more clock cycle:

  test2 <= '1'; -- test1
  test3 <= '1'; -- test2
  test4 <= '1'; -- test3

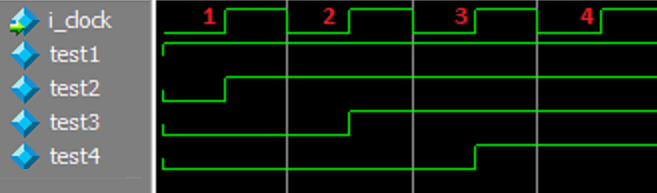
So now at the end of the third clock cycle (beginning of the 4th cycle), test4 will be equal to 1. Therefore it took three full clock cycles for the value of 1 which was initialized in test1 to propagate all the way to test4. See the simulation results below for a verification of this.

Congratulations, you have created sequential logic!

Do you understand clearly why test4 is equal to 1 at the beginning of clock cycle 4 in the screenshot above? I’ll state it here again: test4 transitions to 1 on clock cycle 3, but due to propagation delay it does not become 1 until somewhere between clock cycle 3 and clock cycle 4. Therefore, we must wait until clock cycle 4 to be sure that test4 is equal to 1. Make sure this is clear to you! This is a very important concept in digital design that is completely foreign to software engineers. Reread this example again until this is perfectly understood.

Now at this point you are probably thinking that you understand the basics and you’re ready to code. However, it is critical for you to understand why VHDL and Verilog are different than a normal software programming language. VHDL and Verilog are hardware programming languages! There are three very common mistakes that new FPGA designers make. If you read questions on Stack Overflow you will see these three mistakes over and over and over again by new FPGA designers. If you read this article which explains Hardware Development to Software Engineers and fully understand it, you will be so much happier.

Next up is your first FPGA program: An LED Blinker